数学高考竞赛对接辅导1

高考数学可以轻松应对； 对数学竞赛有兴趣，自发选择学习数学竞赛； 具备自主学习能力； 高考涉及的其他学科不存在太大问题，或个人的竞赛前景远优于高考前景。

数学竞赛需要的时间和精力都是很大的，并且如果因为学习竞赛受挫而导致对数学产生负情绪是得不偿失的，因此，我从不提倡“全民竞赛”。当然，如果你恰好符合以上的四个条件，那么你一定要学习竞赛。为什么？因为学习数学竞赛的好处很多。

与其他学科竞赛一样，学习数学竞赛除了能在升入高校方面获得保送或降分的优惠外，还能培养学生的自主学习能力，这对学生的整个大学学习乃至今后的学术研究或是社会工作是尤为重要的。

当然，对于大部分学生来说，高校的吸引力是最大的。而2016年新发布的高校自主招生政策中，其中的变化值得深思：

取消“校荐”，考生需自己报名； “年级排名”不再是报名条件； 门槛抬高，审核更为严格； 报考专业一定要与特长匹配； 试点高校自主招生考核统一安排在高考结束之后、高考成绩公布前进行。

我们最需要关注的点有三个：

① 由于校荐被取消，年级排名也被废除，原本校内成绩突出的学生很难走自招，而自招的报名人数会上升，竞争更加激烈；

② 据了解，985高校自招的初审底线是竞赛拿到省二以上，而北清更是要求拿到省一，门槛的提高导致了28万申请自招的学生只有4万余人通过初审，8千余人获得资格，初审和复审的通过率均低于20%；

③ 现在的自招考试要求不超过两科，考试的科目和专业是相匹配的，而绝大多数专业的考试科目都有数学，因此数学竞赛的比重是很高的。

总的来说，新的政策直接导致的是各高中年级排名较高的学生更难上清北（难以进入博雅领军，难以获得自招资格，裸考进清北的人更少），而间接导致的是更多的学生走上了竞赛这条道路。因此，若你有足够的实力，精力和时间，那么竞赛将是你们的不二之选。

此外，数学竞赛学到一定深度后就会发现， 数学竞赛不再是由知识结构和解题方法组成，而是对思维能力的培养和运用，而思维能力的价值是远超过数学本身的，这将会对学生以后对问题的思考与对事物的判断等产生不可估量的影响。当然，这是后话。

说归说，高中数学竞赛指的究竟是什么？我想说的是，绝不仅仅是高联（全国高中数学联赛）这么简单。下面，我就带着大家理一理高中阶段可能会遇到的竞赛。

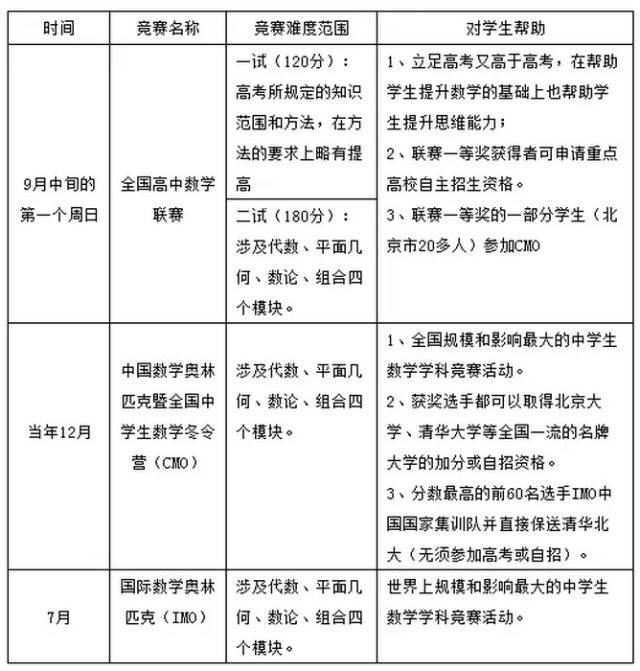
1. 全国高中数学联赛

全国高中数学联赛旨在选拔在数学方面有突出特长的同学，让他们进入全国知名高等学府，而且选拔成绩比较优异的同学进入更高级别的竞赛，直至国际数学奥林匹克（IMO）。并且通过竞赛的方式，培养中学生对于数学的兴趣，让学生们爱好数学，学习数学，激发学生们的钻研精神，独立思考精神以及合作精神。

2.中国数学奥林匹克（CMO）

CMO考试完全模拟IMO进行，每天3道题，限四个半小时完成。每题21分（为IMO试题的3倍，为符合中国人的认知习惯），6个题满分为126分。颁奖与IMO类似，设立一、二、三等奖，分数最高的约前60名选手将组成参加当年国际数学奥林匹克（International Mathematical Olympiad,简称IMO）的中国国家集训队。

3.国际数学奥林匹克（IMO）

国际数学奥林匹克(International Mathematical Olympiad，简称IMO)是世界上规模和影响最大的中学生数学学科竞赛活动。

正如专家们指出：IMO的重大意义之一是促进创造性的思维训练，对于科学技术迅速发展的今天，这种训练尤为重要。数学不仅要教会学生运算技巧，更重要的是培养学生有严密的思维逻辑，有灵活的分析和解决问题的方法。

根据我的感觉，如果高考的数学难度有两星，那么高联的一试难度大概有三颗星，二试难度大概有四颗星；而CMO和IMO的难度大概在五颗星左右。因此，参加高中竞赛的确能够凸显在数学方面的能力，从而获得各大高校的高度关注。

那么问题来了，面对数学竞赛，我们应该如何学习？

首先是全国数学联赛一试，此模块立足于高考又高于高考，题目难时间短，要想攻克此模块需在巩固高考基础的前提下多做难题并分析总结，辅之以足够的模拟训练。

而之后我要详谈的是全国联赛二试以及CMO、IMO的玩法。这里我着重强调四点：

思维启迪

数学竞赛与高考数学的差异不只是在命题大纲上，更表现在思维方式上。 如果说一个在数学方面不是明显太弱的学生，可以通过大量的难题训练来让自己的高考数学成绩提高的话，那么在数学竞赛上这是完全行不通的。从高考数学到竞赛数学，整个思维方式和学习方法的转变，如果没有一位有能力的教练的帮助，必然事倍功半。 很多竞赛高手在后期的能力都是超越当初的入门教练的，但是教练在入门时提供的如何思考、分析、解题和总结的方法却尤为重要。

专题学习与思维养成

这部分一共分为代数、平面几何、数论、组合四个模块，学生应当对四块作专题学习，并在学习过程中熟悉并运用竞赛思维。整个学习过程最后可以有教练引导，但学生的自主学习意愿与自主学习能力尤为重要。

专题分析与训练

竞赛中有很多重要的题型或是模型最好是由教练来点拨，辅之以足够的训练可以收获良好的效果。

赛前模拟

赛前模拟的意义不言自明。

以上四点，主要针对的是备考阶段。而关于如何学习数学竞赛，有什么不同的规划？我根据不同的学生情况，给出了3种不同的方案：

① 初三开始学习高中竞赛

如果孩子学过初中竞赛，并且没有太多中考压力，建议在初三开始学习高中内容（推荐的自学教材为《奥数教程》）。这样的话，在高一刚开学就可以参加一次高联，情况好的话可拿下一试和二试的几何与组合。接下来高一高二两年重点学习二试内容，初期是《奥林匹克小丛书》（小蓝本），往后可以是《奥赛经典》、《命题人讲座》等，并在两个考前的暑假做些赛前模拟。

② 高一开始学习高中竞赛

如果你是从高一开始正式学习高中竞赛，并且定位是省一以上，那么你可能需要把比较多的精力在竞赛上。首先在高一一年里，你必须在一试的难度上学完高中内容，并且对二试有一定的涉及，自学要求为《奥数教程》和《奥林匹克小丛书》（能力过强者可跳过《奥数教程》），然后第二年再进行更强的学习，攻克《命题人讲座》等。

③ 高二开始学习高中竞赛

如果你是从高二开始正式学竞赛，那么前提是你必须已经具备比较强的一试功底，然后攻克《奥林匹克小丛书》和《命题人讲座》。并且一般来说由于竞争对手们过于强大，你的定位一般是省一和自招。（当然也不绝对，笔者当年就是从高二开始学的，通过努力，冲进国集也是有可能的）。

正所谓“春暖花开谈恋爱，不如一心一意搞竞赛”，学竞赛注定是一个孤独而有趣的过程。高考党更多是出于外界的设定如选择了高考，但竞赛党一定是因为自己的兴趣而选择了竞赛。多年之后，你可能会忘了竞赛题该怎么去解，也可能会忘了什么是柯西不等式或者费马小定理，但是你不会忘记你在解题过程中学会的这种思维方式和习惯，更不会忘记自己曾经在一个十六七岁的年纪，就为了某个自己喜欢的东西而奋不顾身追寻的这一腔热血。以上正是学习数学竞赛的四个境界。

附：高中数学竞赛大纲（2006年修订版）

全国高中数学联赛

全国高中数学联赛（一试）所涉及的知识范围不超出教育部2000年《全日制普通高级中学数学教学大纲》中所规定的教学要求和内容，但在方法的要求上有所提高。

全国高中数学联赛加试

全国高中数学联赛加试（二试）与国际数学奥林匹克接轨，在知识方面有所扩展；适当增加一些教学大纲之外的内容，所增加的内容是：

1、平面几何

几个重要定理：梅涅劳斯定理、塞瓦定理、托勒密定理、西姆松定理。

三角形中的几个特殊点：旁心、费马点，欧拉线。

几何不等式。

几何极值问题。

几何中的变换：对称、平移、旋转。

圆的幂和根轴。

面积方法，复数方法，向量方法，解析几何方法。

2、代数

周期函数，带绝对值的函数。

三角公式，三角恒等式，三角方程，三角不等式，反三角函数。

递归，递归数列及其性质，一阶、二阶线性常系数递归数列的通项公式。

第二数学归纳法。

平均值不等式，柯西不等式，排序不等式，切比雪夫不等式，一元凸函数。

复数及其指数形式、三角形式，欧拉公式、棣莫弗定理，单位根。

多项式的除法定理、因式分解定理，多项式的相等，整系数多项式的有理根*，多项式的插值公式*。

n 次多项式根的个数，根与系数的关系，实系数多项式虚根成对定理。

函数迭代，简单的函数方程*。

3、初等数论

同余，欧几里得算法，裴蜀定理，完全剩余类，二次剩余，不定方程和方程组，高斯函数 [x]，费马小定理，格点及其性质，无穷递降法，欧拉定理*，孙子定理*。