高中数学知识点,高中数学重点知识归纳

“参考和证明”是数学的基本思维过程，也是人们在学习和生活中经常使用的思维方式。推理通常包括合理推理和演绎推理。合理推理是一种推理过程，可以基于现有事实和正确结论，实验和实践的结果以及个人经验和直觉来推断某些结果。归纳法和类比法是进行合理推理的常用思维方法。在解决问题的过程中，明智的推理具有猜测和发现结论，探索和提供思想的功能，有利于创新意识的培养。演绎推理是一种推理过程，在该过程中，将基于现有事实得出新结论，并根据严格的逻辑规则得出正确的结论。培养和提高学生的演绎推理或逻辑证明能力是高中数学门课程的重要目标。合理推理与演绎推理之间的联系是紧密而互补的。证明通常包括逻辑证明以及实验和实践证明，但是数学结论的正确性必须通过演绎推理或逻辑证明来保证，也就是说，在正确前提的基础上，可以通过正确使用推理规则来得出结论。在本单元中，学生将通过回顾所学知识，进一步体验合理的推理，演绎推理以及两者之间的联系和区别；体验数学证明的特征，了解数学证明的基本方法，包括直接证明方法（例如分析，综合）和间接方法（例如矛盾），感受逻辑证明在数学和日常生活中的作用，并发展推理和证据的习惯。

首先，在高中数学中，收集了初步知识以及与其他内容的紧密联系。它们是学习，掌握和使用数学语言的基础，也是高中数学学习的起点。在教学中，要注意引导学生更好地理解数学中出现的集体语言，使学生可以更好地利用集体语言表达数学问题，使学生能够运用集体观点研究和处理数学问题。因此，集合的基本概念，功能和其他相关内容就是老师关注的内容。

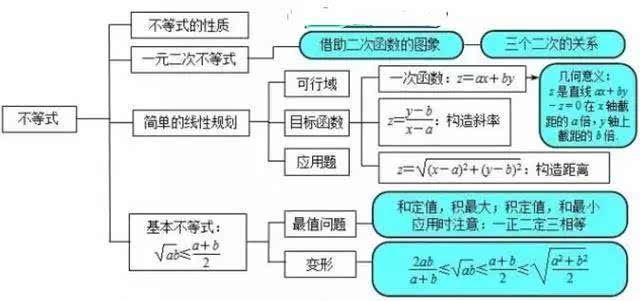
高考数学平面解析几何问题解决方法高考数学知识点大全高考数学平面解析几何学习方法！在高中数学知识系统中，平面解析几何占很大一部分，涉及直线及其方程，线性规划，圆及其方程，椭圆及其方程，抛物线及其方程，双曲线及其方程以及曲线和方程关系的具体介绍

及其图像：高中数学学习由从浅到深的零散知识点组成，其测试将各种知识整合为一个完整的测试题。近年来，随着“新高考”政策的实施，数学考试也发生了一些变化。文科科目知识点也根据该省新的高考政策选择。接下来，我们将简要总结高中数学知识点，希望为即将入学或正在读高中的学生提供一些帮助。

没有进一步研究的条件。 高中数学与初中数学相比，深度，知识广度和能力要求是一个飞跃。这需要掌握基础知识和技能，为进一步的学习做准备。 高中数学许多地方都很困难，方法又新又要求分析能力。例如封闭区间内二次函数的最大值，函数范围的计算，实根和参数方程的分布，三角公式的变形和灵活使用，空间概念的形成以及置换的应用以及组合问题和实际应用问题。客观地讲，这些观点是不同的。某些内容仍与高中和初中教科书未涵盖的内容无关。如果不采取补救措施，区别是不可避免的。

高中数学知识点：圆形区域的面积是多少？圆形的周长是多少？如何找到圆的周长和面积？圆的公式是什么？以下组合教育编辑器将对其进行分析，仅供您参考。圆的周长公式的面积公式是多少？圆的周长公式=直径×周长比或圆周长=半径×2×周长字母

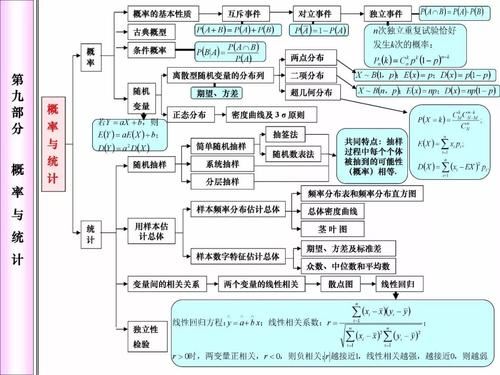
高中数学：特殊角度的三角函数值表重要的一点是，通常的三角函数在平面直角坐标系中定义，并且它的定义域是整个实数域。下面的组合教育老师张老师编了《特殊角度的三角函数值表》供学生参考！特殊角度函数值表的图表相关方程式由数字

组合教育精心汇编的30个数学必修公式和知识，可以帮助您测试另外20点！今天，来自联合教育的张先生为每个人编写了高中数学考试知识点的必要公式，快来看吧！ ！函数的单调性，函数的奇偶性，导数在某个位置的几何含义，几个常用函数的导数算法，一个函数的最高分指数是

。学习内容：数字序列，三角函数，实体几何，概率统计，圆锥曲线，导数，参数方程式和不等式。似乎并没有很多，但是每个部分都涵盖了许多关键点和困难，这需要我们花费一些时间进行梳理。互联网上有许多树形图和列表可供每个人参考，但掌握知识点不是最重要的。最重要的是如何利用从问题中获得的知识，这要求我们在老师的带领下进行练习。 。我该如何做

高中数学试卷？我的习惯是用模拟问题进行主题练习，即，我复习三角函数，每天做五组纸质函数，练习多项选择题，并使用多项选择题。高考卷是完全模拟的，并且优先考虑在我自己的省以及与我自己的省类似的州对卷进行模拟。时间跨度为三年内。因为我是课程改革的第二年，所以论文的第一年我都很细致。